Математика может быть не только сложной и абстрактной наукой, но и вдохновением для творчества. Создание узоров и рисунков с использованием математических принципов является увлекательным занятием, которое поможет развить ваше воображение и логическое мышление. В этой статье мы представим вам некоторые из самых интересных и красивых узоров, созданных с помощью математики.
.jpg)


.png)













Узоры в геометрии
Геометрия - это раздел математики, который изучает формы, размеры, отношения и свойства пространства. Многие узоры основаны на геометрических фигурах и принципах. Например, узоры Фибоначчи основаны на числовой последовательности, которая строится с помощью сложения двух предыдущих чисел: 1, 1, 2, 3, 5, 8, 13 и т.д. Эта последовательность может быть использована для создания красивых и симметричных узоров.
Другим примером является узор Манделброта, который создается с помощью итерационной функции в комплексной плоскости. Узор Манделброта имеет сложную структуру, состоящую из множества самоподобных форм, и его красота завораживает многих.













Узоры в алгебре
Алгебра - это раздел математики, который изучает структуры и операции над числами. В алгебре также можно создавать узоры и рисунки. Например, фракталы Жюлиа и Мандельброта создаются с помощью итерационных функций над комплексными числами. Эти фракталы имеют сложные и красивые узоры, которые могут быть исследованы в деталях.
Другим примером является узор Серпинского, который создается путем деления треугольника на более мелкие треугольники и удаления некоторых частей. Этот процесс повторяется бесконечное количество раз, и в результате получается самоподобный узор, который имеет фрактальную структуру.

.jpeg)




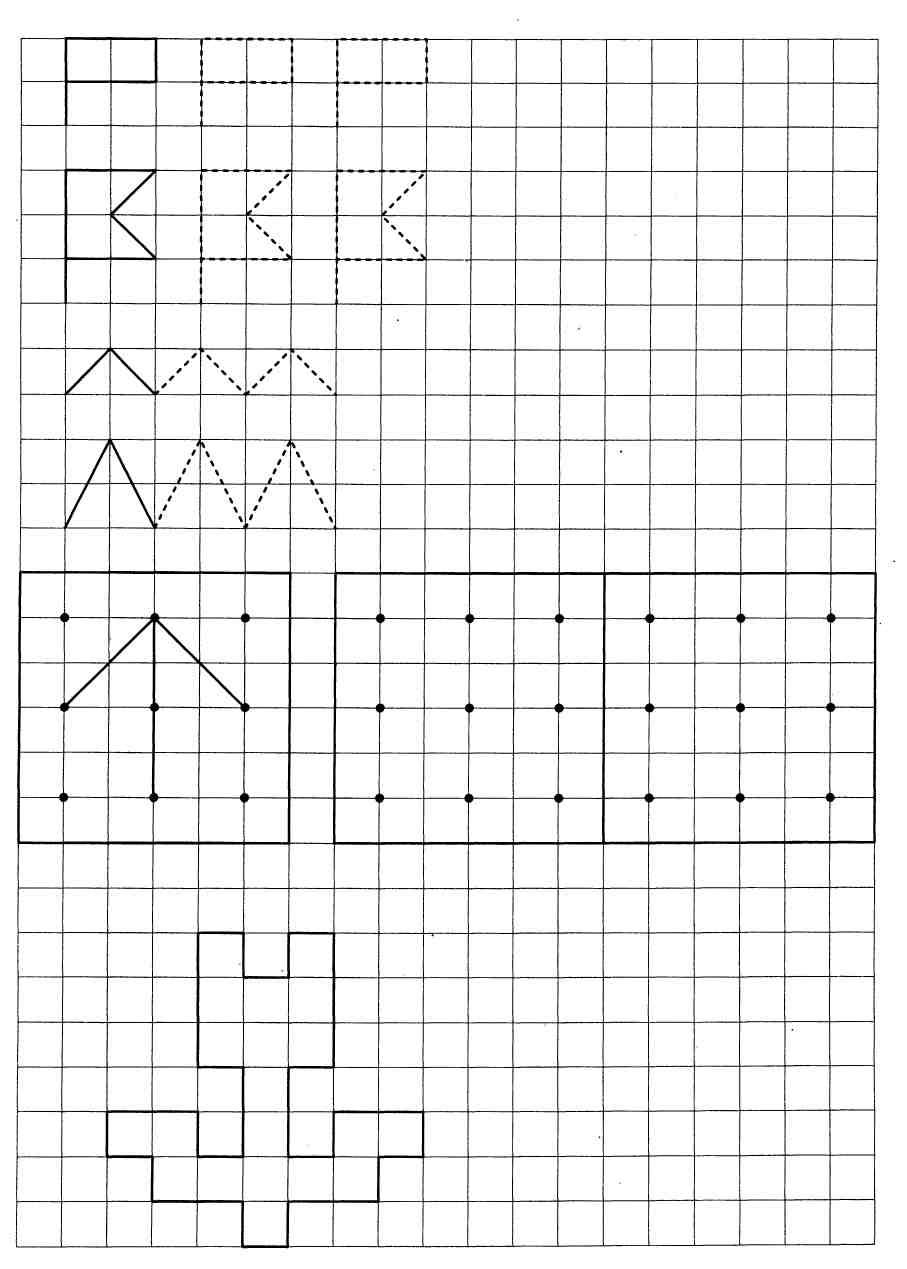
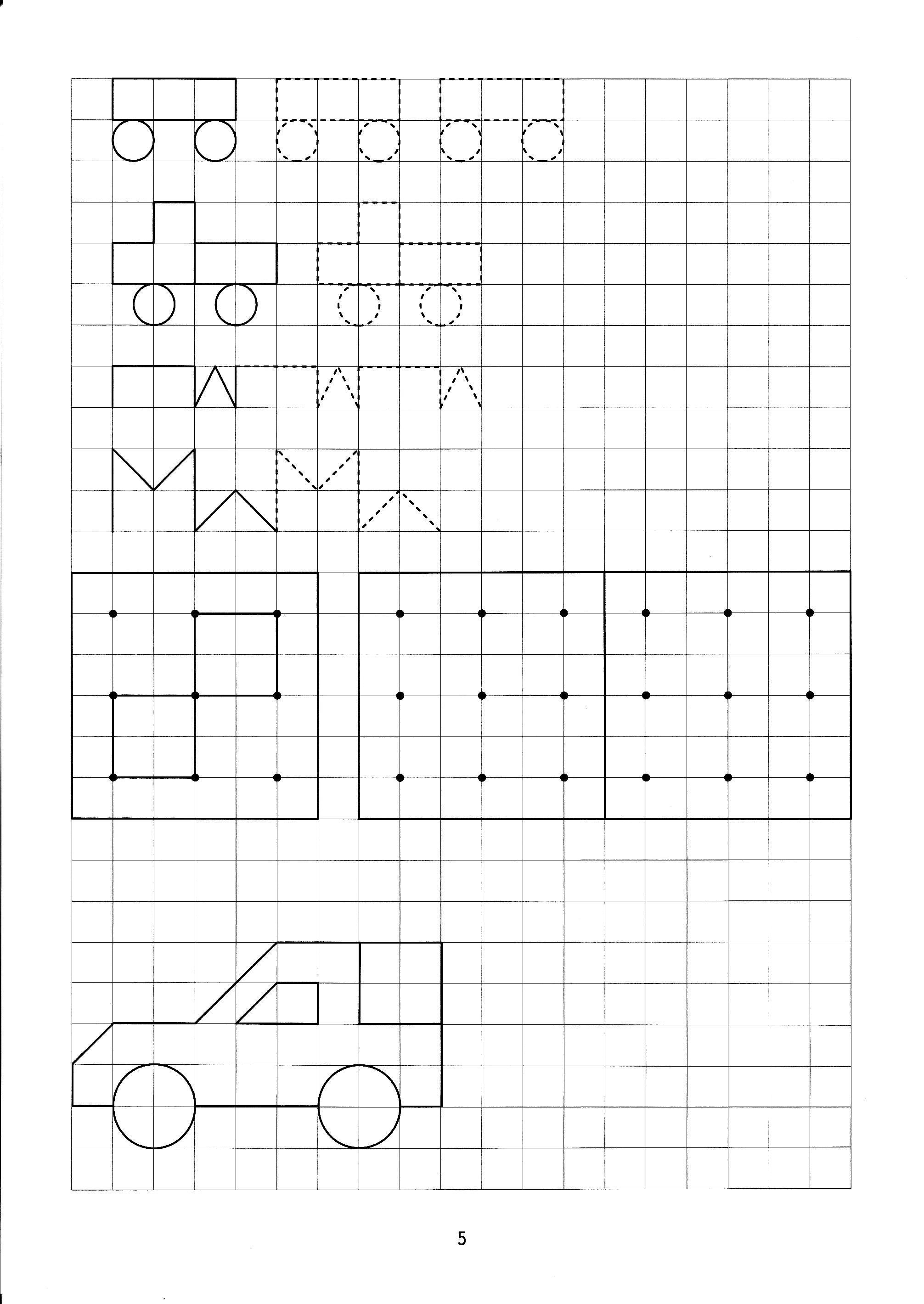
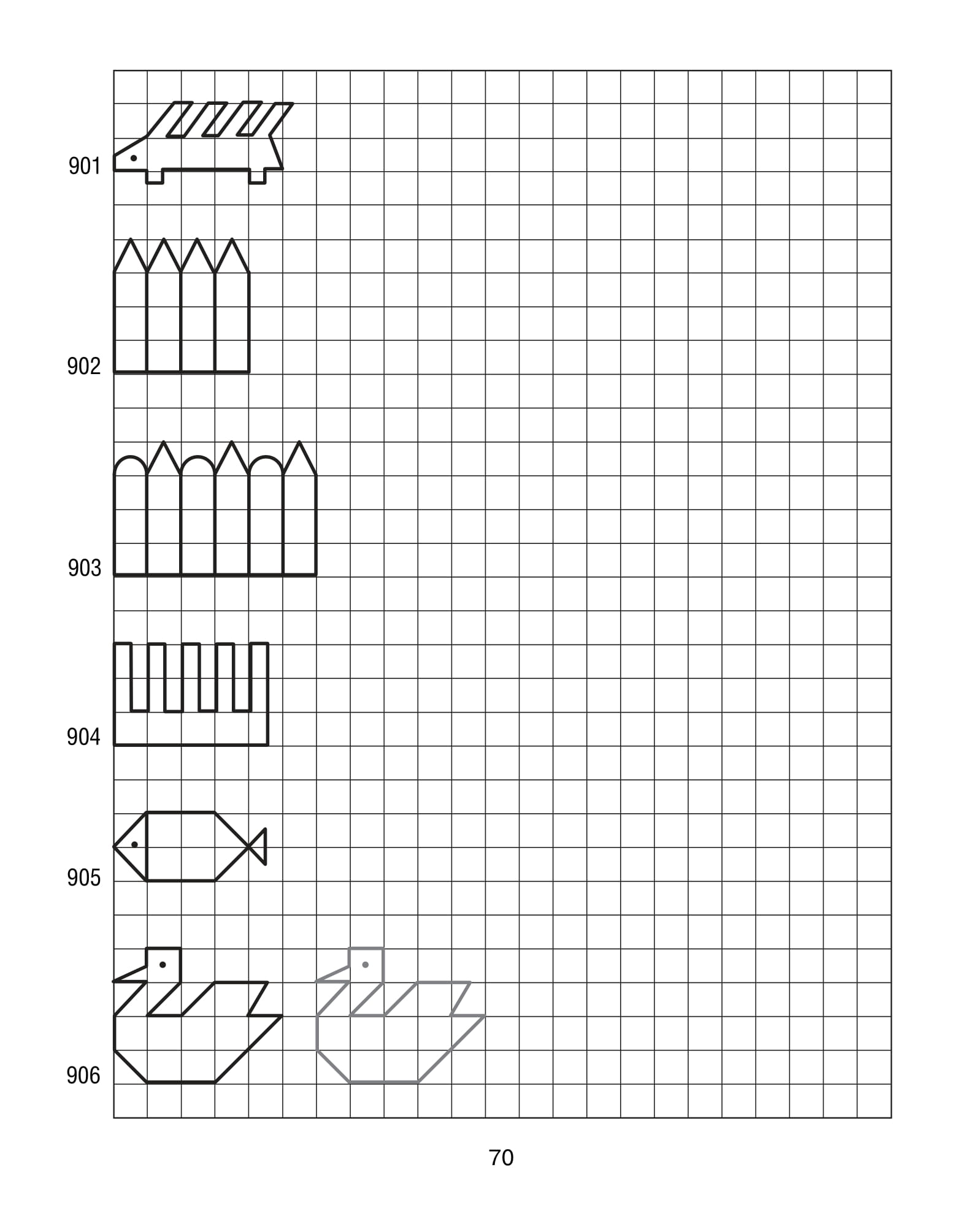
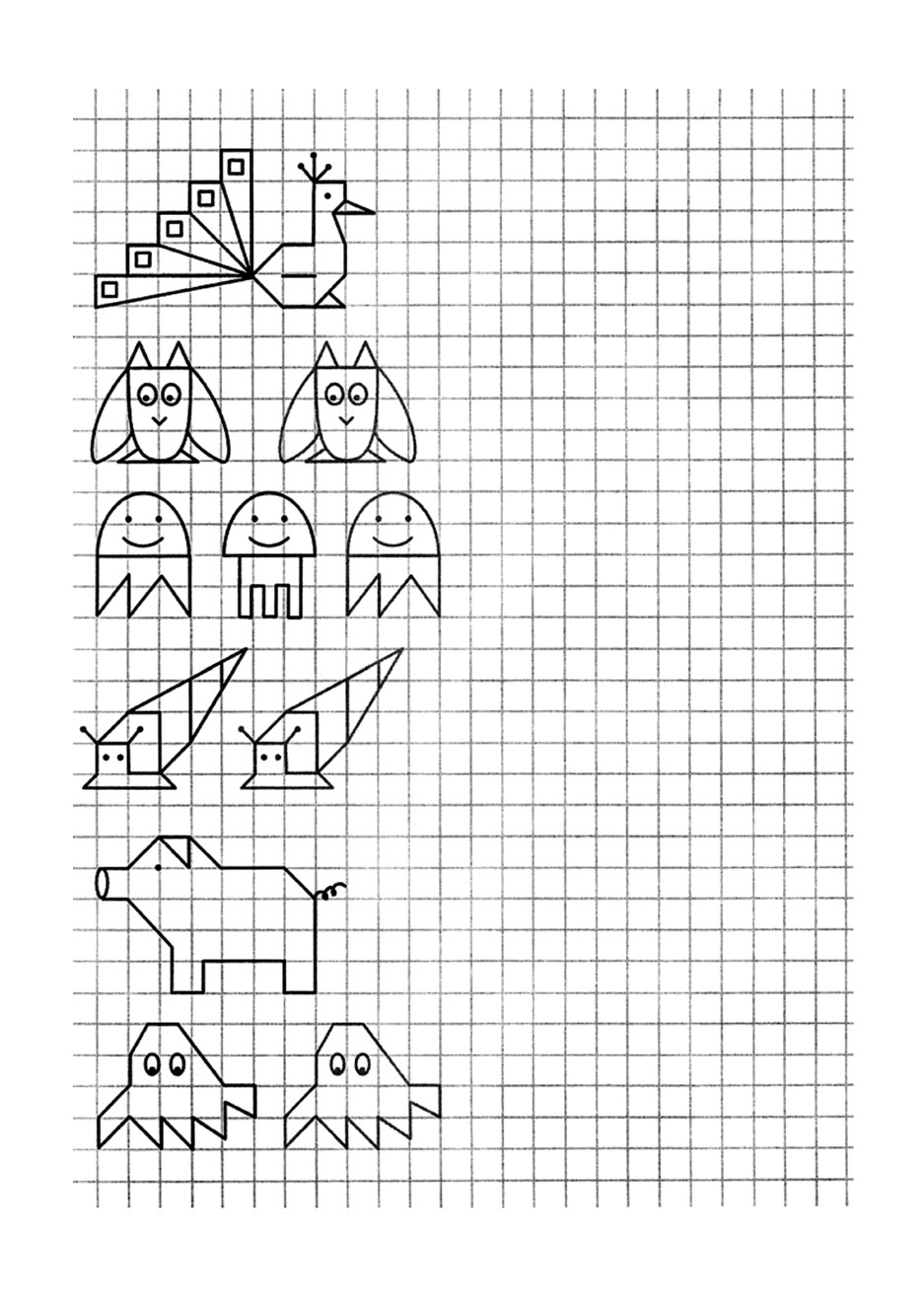












Узоры в теории чисел
Теория чисел - это раздел математики, который изучает свойства чисел и их взаимосвязи. В теории чисел также можно найти интересные узоры и рисунки. Например, узоры Паскаля - это треугольник чисел, где каждое число равно сумме двух чисел над ним в предыдущем ряду. Этот треугольник обладает интересными свойствами и может быть использован для создания узоров и рисунков.
Еще одним примером является узор Улама, который создается путем выделения простых чисел на числовой оси. Простые числа образуют спиральный узор, который имеет интересную структуру и может быть исследован в деталях.






















Заключение
Узоры и рисунки, созданные с помощью математики, могут быть удивительно красивыми и интересными. Они позволяют нам увидеть математику в новом свете и раскрыть ее творческий потенциал. Надеюсь, что вам понравилась эта статья, и вы найдете вдохновение для создания своих собственных математических узоров и рисунков!