Мы часто восхищаемся красивыми узорами и орнаментами, которые видим повсюду: на одежде, посуде, стенах зданий и даже в природе. Но мало кто задумывается о том, что эти рисунки имеют глубокую связь с математикой. В этой статье мы рассмотрим различные узоры и орнаменты, исследуем их математические основы и рассмотрим, как они влияют на нашу жизнь.












Узоры и симметрия
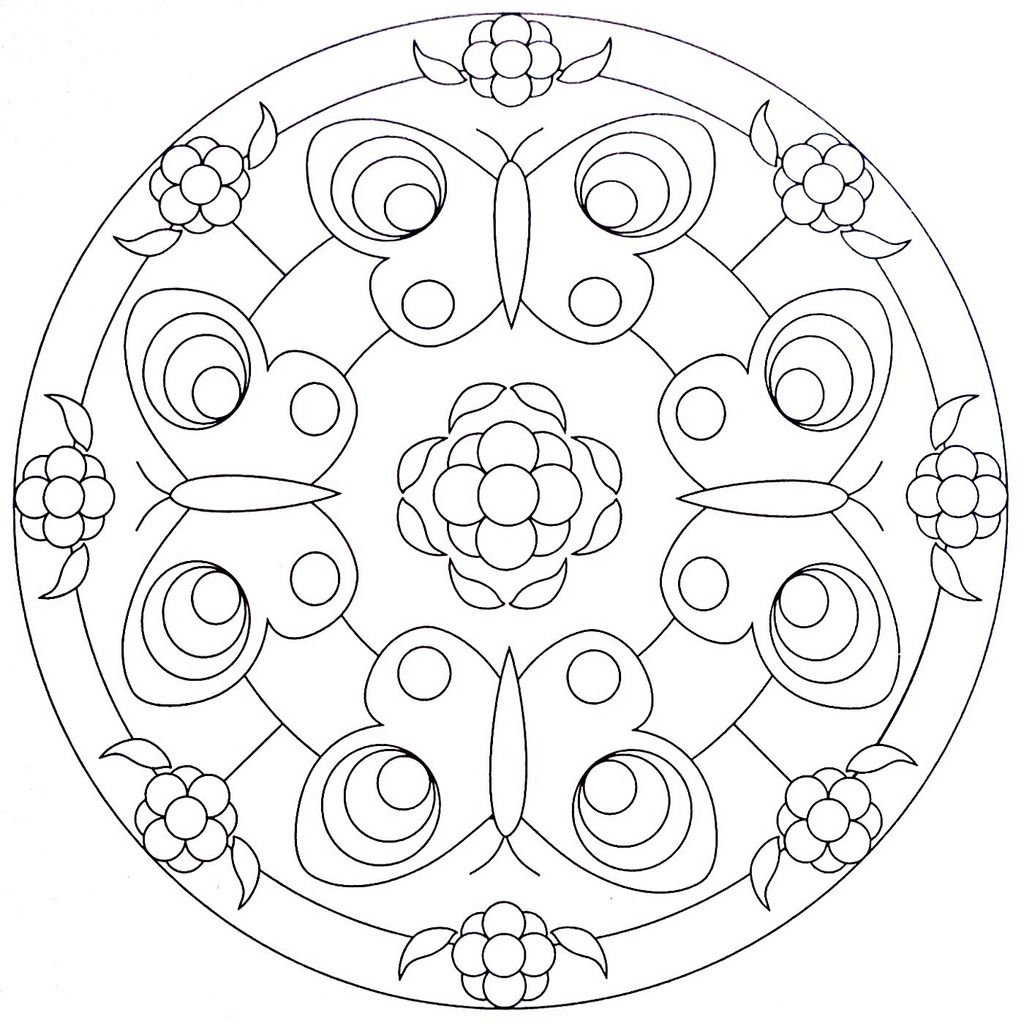
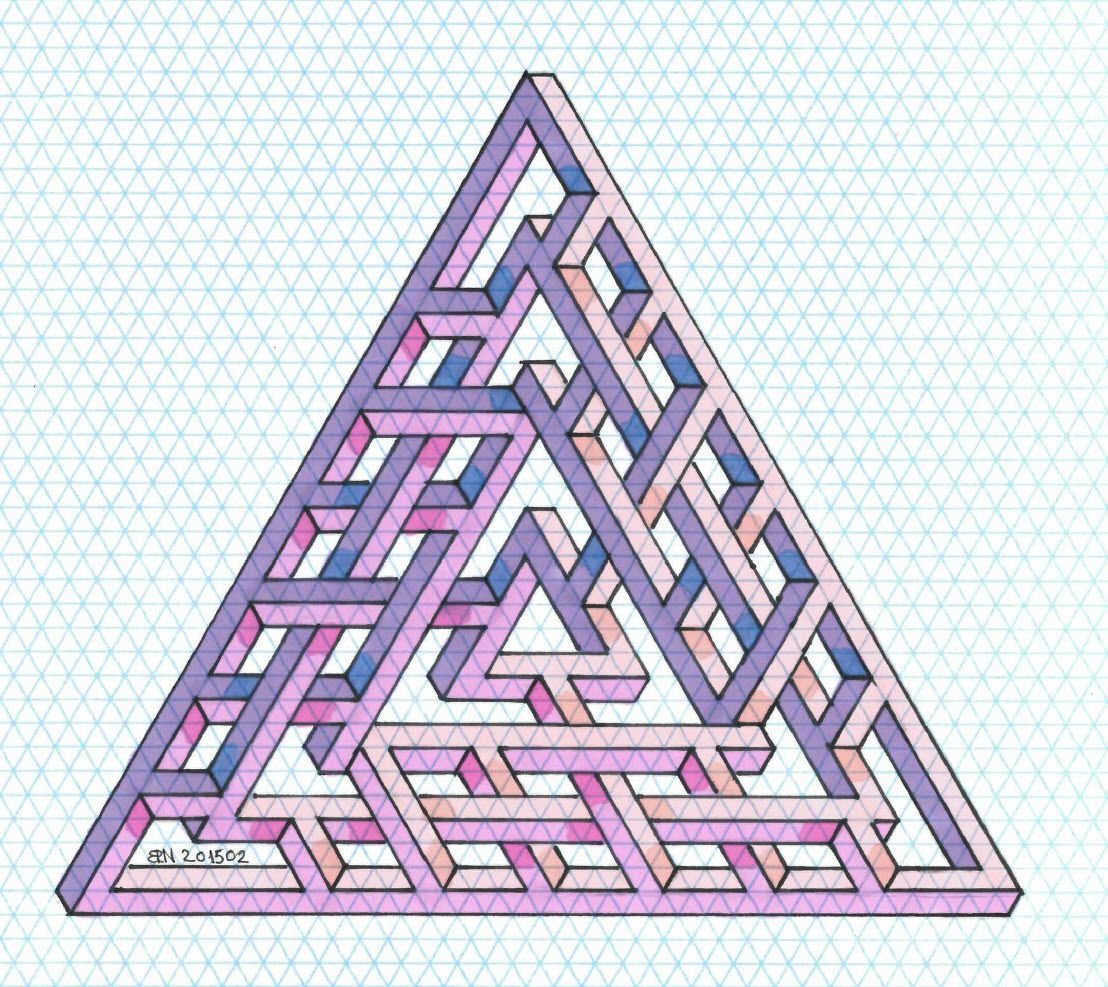
Одной из основных характеристик узоров является симметрия. Симметрия может быть осевой, плоской или центральной. Осевая симметрия означает, что узор можно разделить на две равные части зеркально относительно одной оси. Плоская симметрия означает, что узор можно совместить с его зеркальным отражением. Центральная симметрия означает, что узор можно разделить на две равные части относительно одной точки.






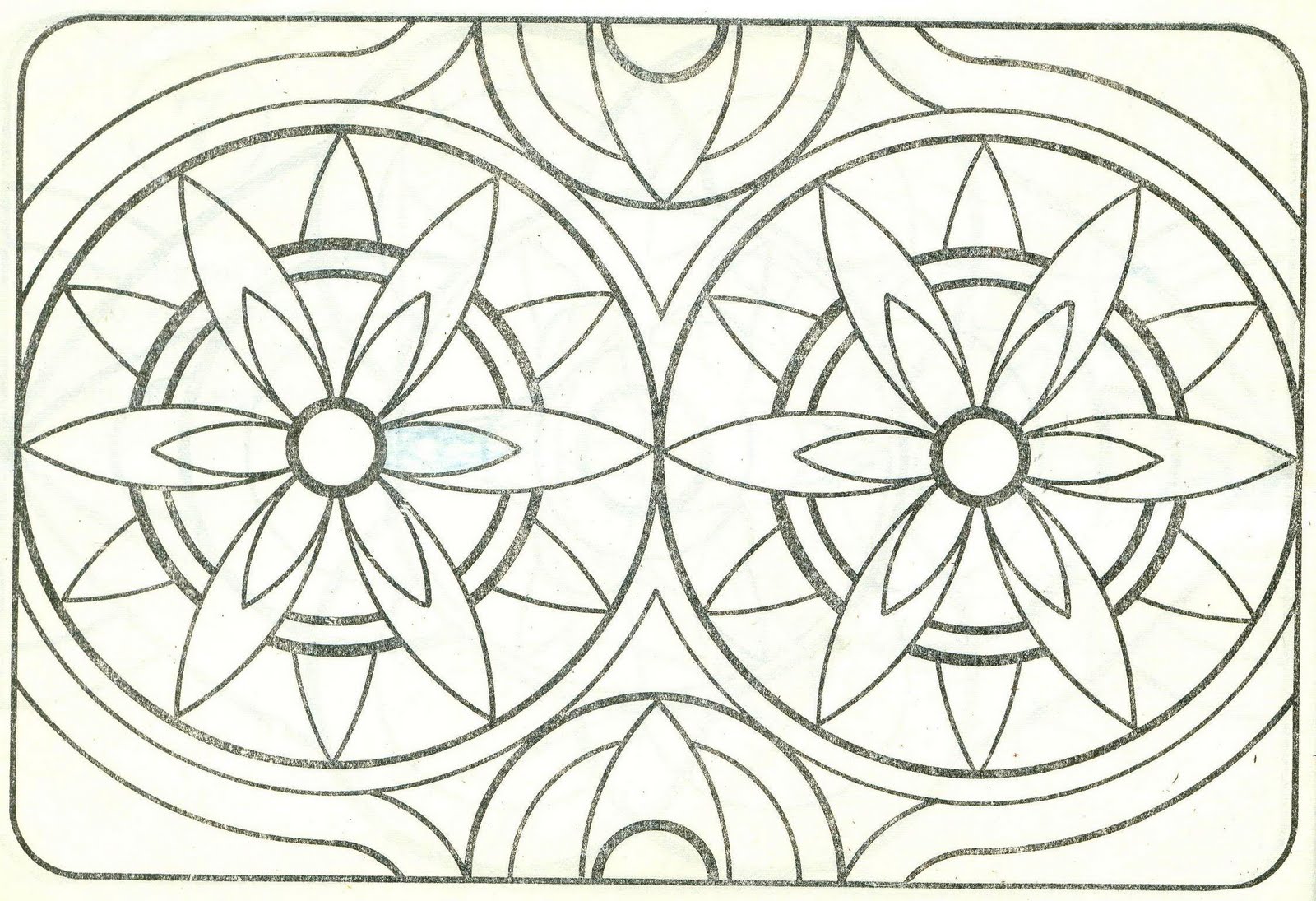









Фракталы и самоподобие
Фракталы - это узоры, которые повторяются в себе на разных масштабах. Они обладают свойством самоподобия, то есть их части имеют сходную структуру с целым. Фракталы можно наблюдать в природе, например, в форме листьев деревьев или в контурах горных цепей. Математически фракталы описываются через рекурсивные формулы и алгоритмы, которые позволяют создавать узоры с бесконечной детализацией.

.jpg)













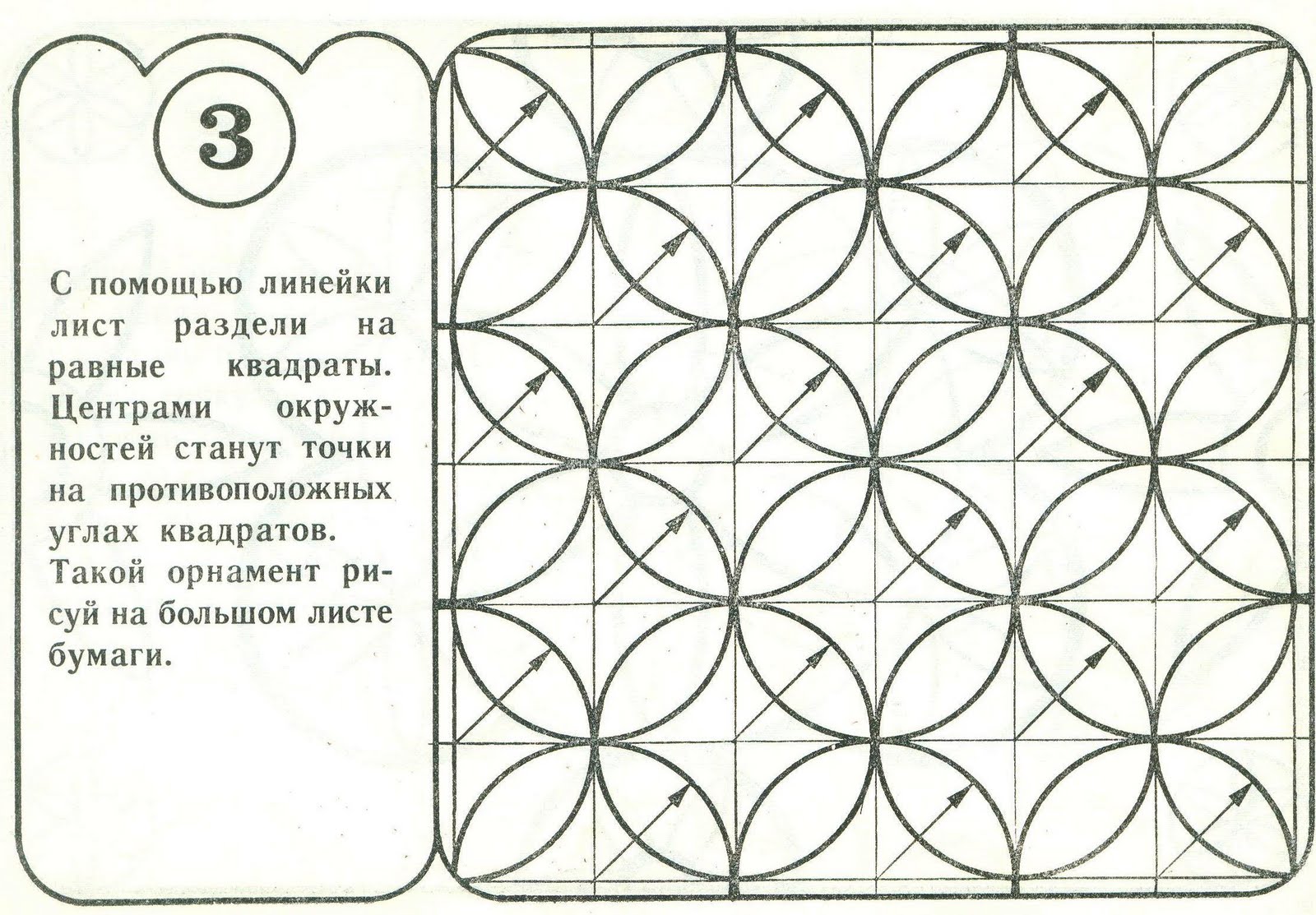
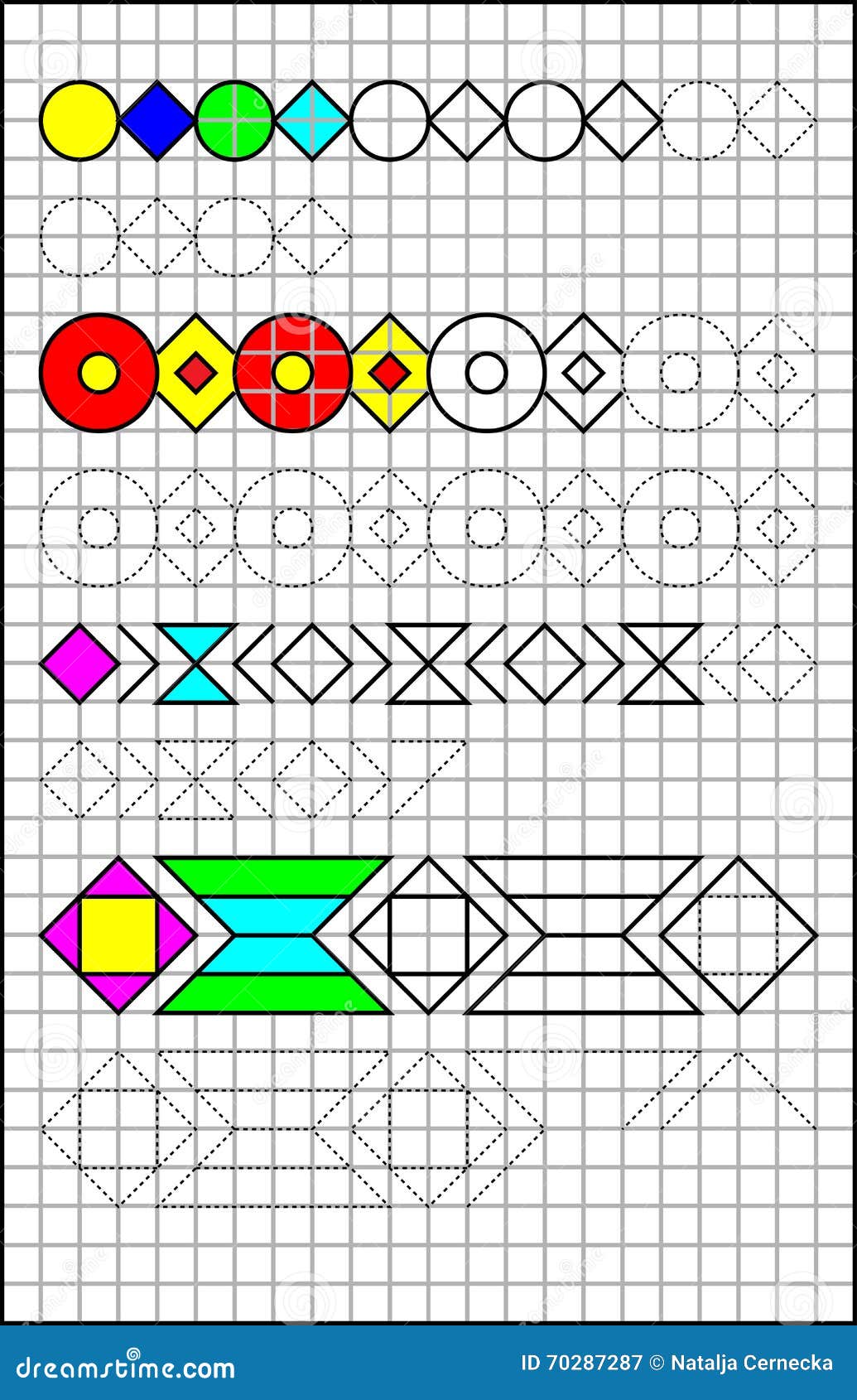
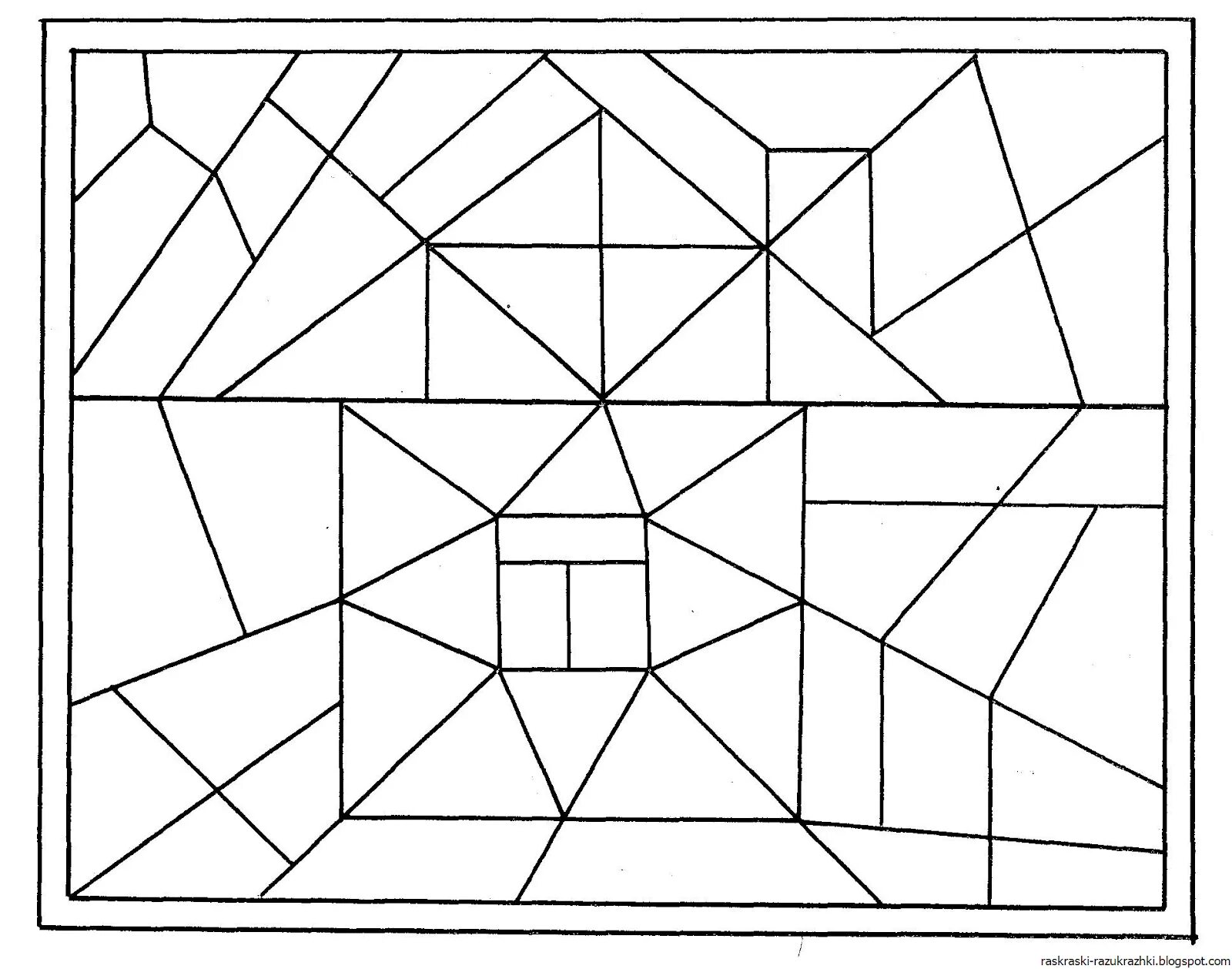
Геометрические узоры
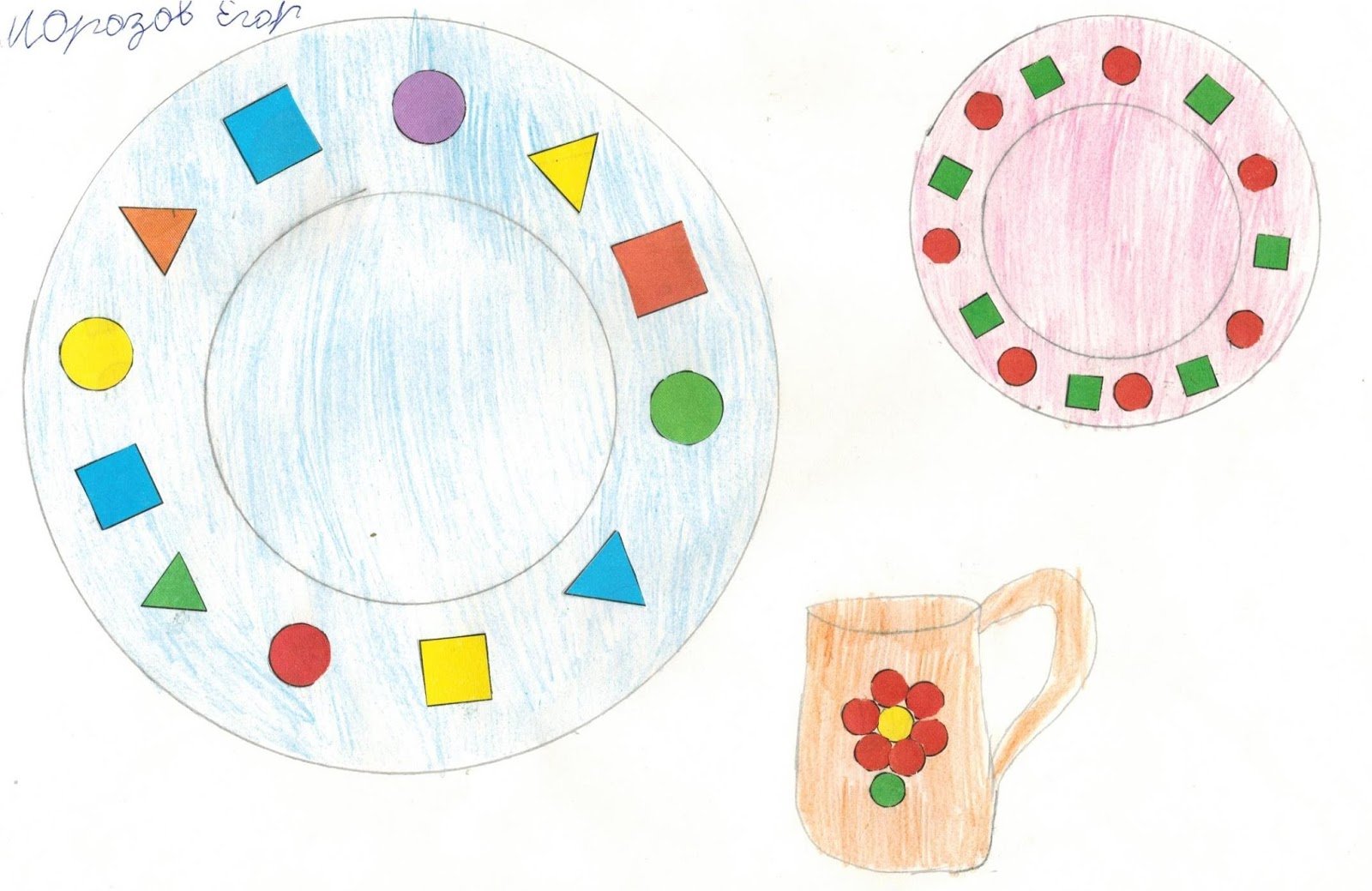
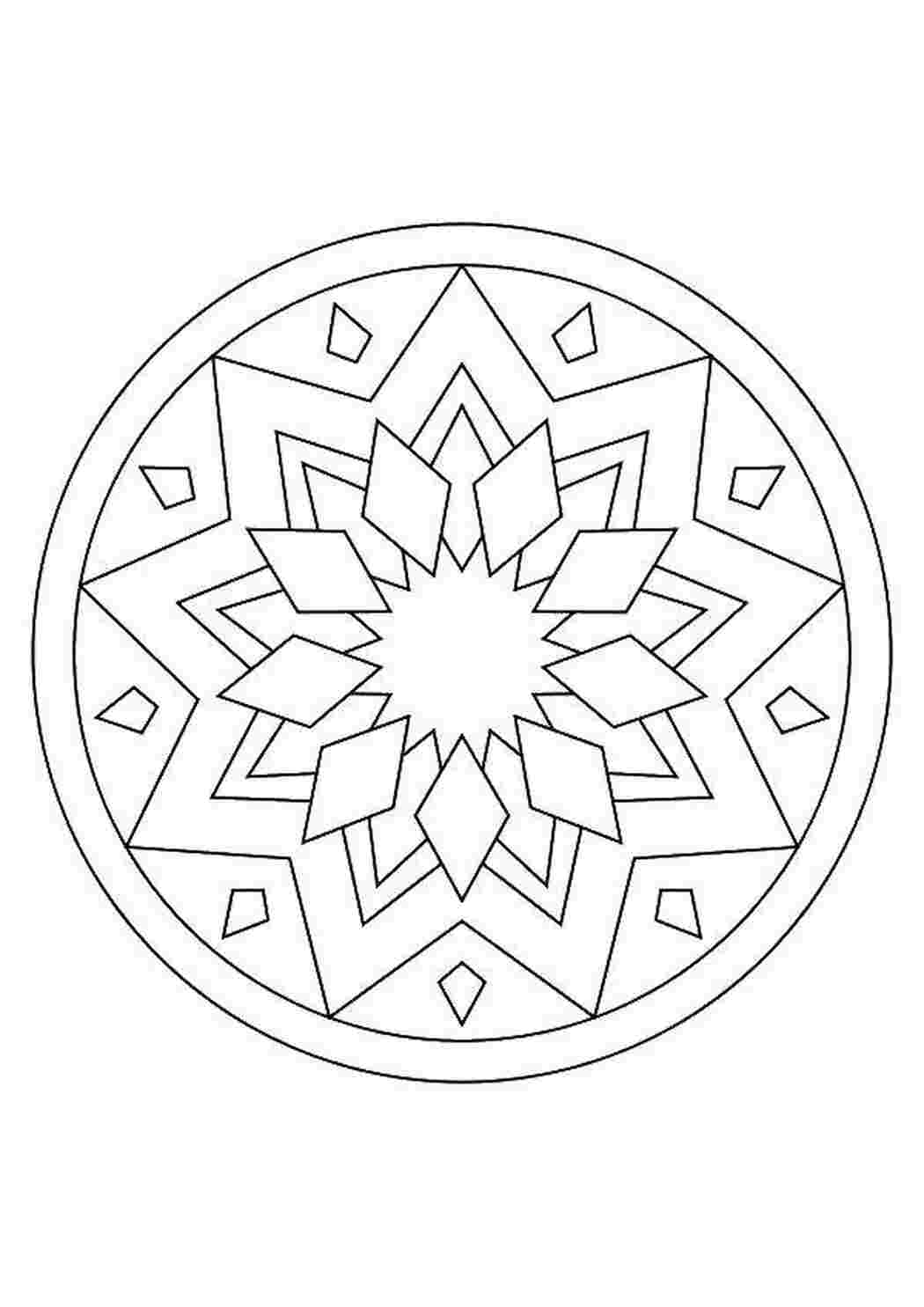
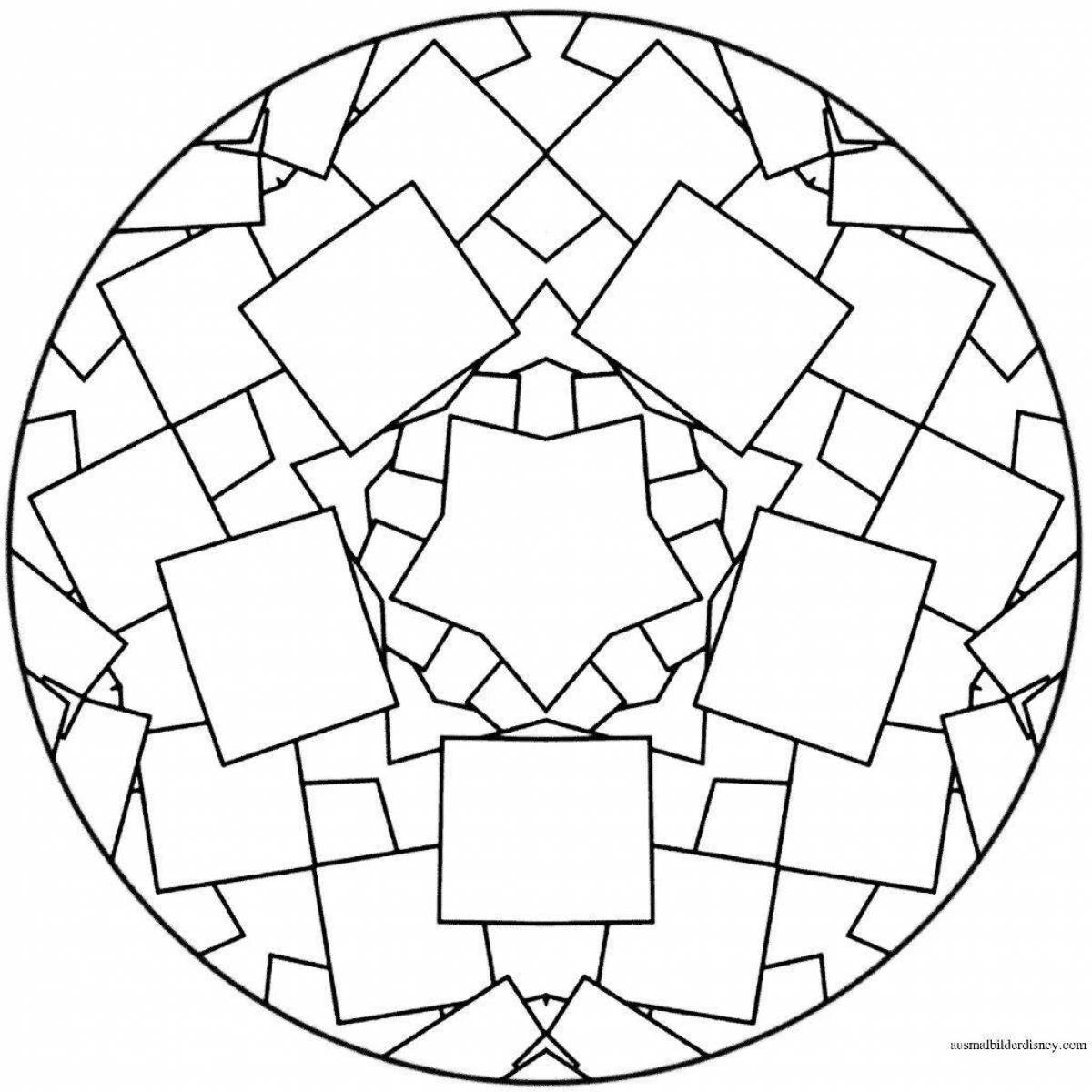
Многие узоры и орнаменты основаны на геометрических фигурах, таких как круги, прямоугольники, треугольники и многоугольники. Геометрические узоры могут быть симметричными или асимметричными, а также могут использовать различные комбинации и повторения фигур для создания интересных композиций.










.jpg)



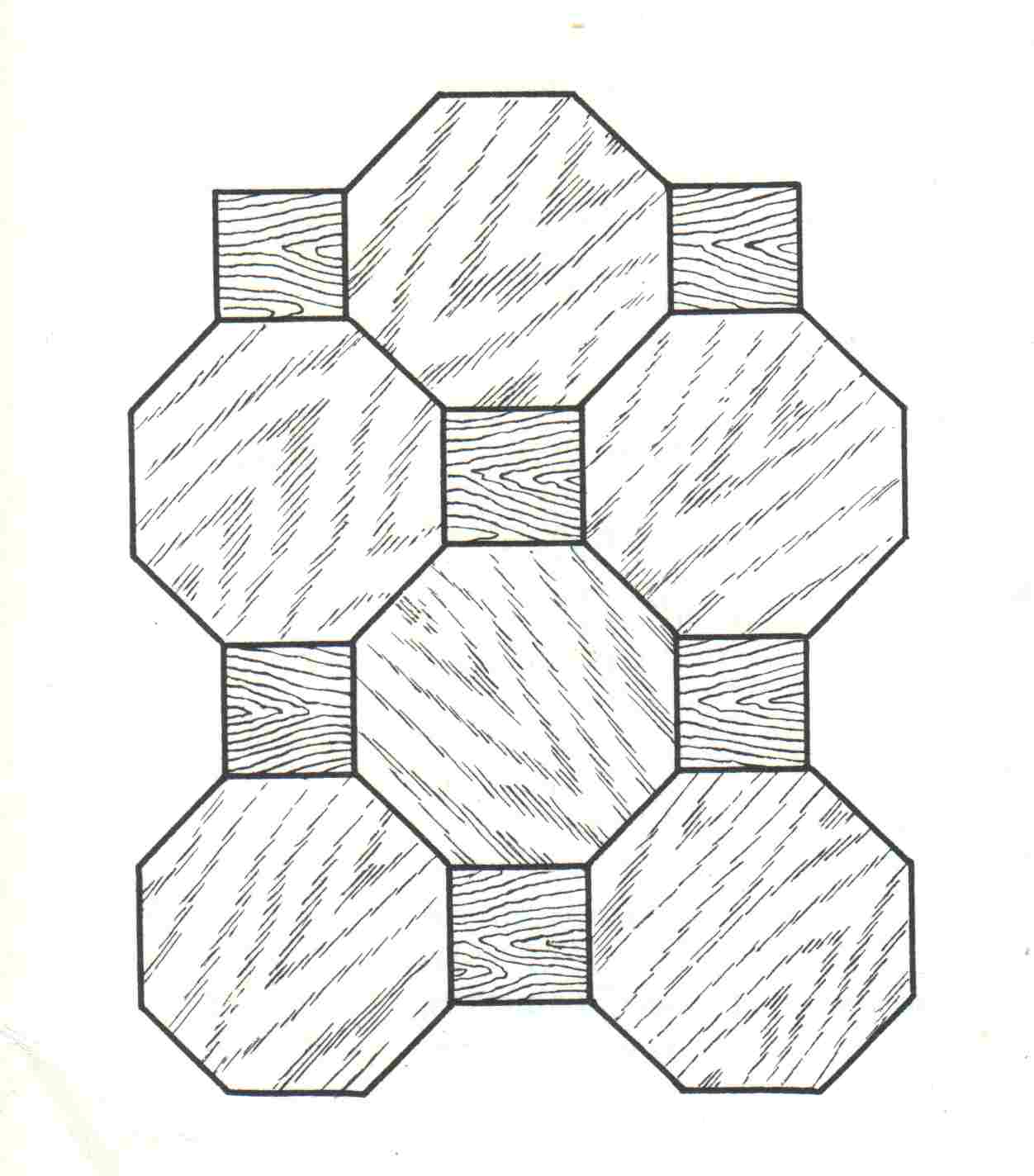
Мозаика и плитка
Мозаика и плитка - это один из самых древних способов создания узоров. Они состоят из множества маленьких элементов, которые объединены в большую композицию. Мозаичные узоры могут быть геометрическими или абстрактными, и часто используются для украшения интерьеров и экстерьеров зданий.














Узоры в природе
Природа также является источником вдохновения для создания узоров и орнаментов. Мы можем наблюдать узоры в текстуре кожи животных, в узоре песка на пляже или в форме снежинок. Природные узоры часто имеют математическую основу, такую как фрактальная структура или геометрические принципы.













Заключение
Узоры и орнаменты окружают нас повсюду и имеют глубокую связь с математикой. Они воплощают принципы симметрии, фракталов и геометрии. Рассматривая узоры и исследуя их математическую природу, мы можем лучше понять и оценить красоту и гармонию, которые они приносят в нашу жизнь.